2025-06-15 APCS 解題紀錄
舊制 APCS 最後一次考試,兩個學生都有去考,既然上課也會需要講解,就順便分享個題解吧!
P1. 小心陷阱
Zerojudge 連結:https://zerojudge.tw/ShowProblem?problemid=q836
解題思路
這題蠻明顯是直接模擬即可,注意要先移動再扣血,且扣血只需用兩個 if 即可處理若同時是 x1 和 x2 的倍數,生命值總共減少 y1 + y2這條規則,用 else if 需多判斷一次且要將此規則提到最前,才能避免只扣到 y1 沒扣到 y2。
Sample Code(C++)
#include <iostream>
using namespace std;
int main() {
int k, x1, x2, y1, y2;
while(cin >> k >> x1 >> y1 >> x2 >> y2) {
int p = 0;
while(k > 0) {
p += k;
if (p % x1 == 0) k -= y1;
if (p % x2 == 0) k -= y2;
}
cout << p << endl;
}
}Sample Code(Python)
k = int(input())
x1, y1 = map(int, input().split())
x2, y2 = map(int, input().split())
p = 0
while k > 0:
p += k
if p % x1 == 0:
k -= y1
if p % x2 == 0:
k -= y2
print(p)P2. 轉盤得分
Zerojudge 連結:https://zerojudge.tw/ShowProblem?problemid=q837
解題思路
這題做法蠻多的,先提供兩個做法,另外有點雷的是題目敘述的轉向和範例的轉向有點容易搞混,若沒有養成讀完題目先用範測驗證思路的習慣,應該會浪費不少時間在 debug 的。
暴力解
觀察範圍 m, n, k <= 30,直接暴力做轉字串可過,另外可以發現轉動距離範圍可以到正負 100,但字串長度最多就 30,所以能取模避免無效轉動。
字串轉法要處理 index out of range 問題會有點麻煩,實作上個人習慣直接將字串複製一遍,這樣要從 [0, n) 開始取 n 個字,結尾 index 必定落在 [n-1, 2*n) 之間。
計數部分 C++ 用 unordered_map,Python 則用 Counter。
Sample Code(C++)
#include <iostream>
#include <unordered_map>
using namespace std;
int main() {
int m, n, k;
while(cin >> m >> n >> k) {
string s[m];
for(int i=0; i<m; i++) cin >> s[i];
int ans = 0;
while(k--) {
for(int i=0, x; i<m; i++) {
cin >> x;
x %= n; // 或是 (x % n + n) % n,就能統一底下的轉法
s[i] += s[i];
if (x > 0) s[i] = s[i].substr(n-x, n);
else s[i] = s[i].substr(-x, n);
}
unordered_map<char, int>mp;
char maxi = 'a';
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
mp[s[j][i]]++;
if (mp[s[j][i]] > mp[maxi]) maxi = s[j][i];
}
ans += mp[maxi];
mp.clear();
}
}
cout << ans << endl;
}
}Sample Code(Python)
from collections import Counter
m, n, k = map(int, input().split())
s = [input() for _ in range(m)]
ans = 0
for _ in range(k):
shift = list(map(int, input().split()))
for i in range(m):
shift[i] %= n
s[i] = (s[i] * 2)[n-shift[i]:n*2-shift[i]]
ans += sum([max(Counter(c).values()) for c in zip(*s)])
print(ans)優化解
只紀錄 index 的移動,可以節省字串操作的時間,實作小心不要取錯 index。
題外話,這題 n, m 小到優化解因為取模量更多,導致沒快多少,甚至 python 有些 case 更慢…。
Sample Code(C++)
#include <iostream>
#include <cstring>
#include <unordered_map>
using namespace std;
int main() {
int m, n, k;
while(cin >> m >> n >> k) {
string s[m];
int shift[m];
memset(shift, 0, sizeof(shift));
for(int i=0; i<m; i++) cin >> s[i];
int ans = 0;
while(k--) {
for(int i=0, x; i<m; i++) {
cin >> x;
shift[i] = ((shift[i] - x) % n + n) % n;
}
unordered_map<char, int>counter;
char maxi = 'a';
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
char c = s[j][(i + shift[j]) % n];
counter[c]++;
if (counter[c] > counter[maxi]) maxi = c;
}
ans += counter[maxi];
counter.clear();
}
}
cout << ans << endl;
}
}Sample Code(Python)
from collections import Counter
m, n, k = map(int, input().split())
s = [input() for _ in range(m)]
shift = [0] * m
ans = 0
for _ in range(k):
shift = [(x - y) % n for x, y in zip(shift, map(int, input().split()))]
ans += sum([max(Counter(c[(i+x)%n] for c, x in zip(s, shift)).values()) for i in range(n)])
print(ans)P3. 貪心闖關
Zerojudge 連結:https://zerojudge.tw/ShowProblem?problemid=q838
這題開始只附上 C++ 版本,目前我自己收的 APCS 3->5 學生是不教 Python 的(絕對不是因為我懶)。
解題思路
這題一樣有很多種解法,這裡提供 heap + map 和 multiset 的解法,競賽選手的話應該能想到線段樹甚至砸 treap,但這兩個都超綱了不提。
另外注意 overflow 問題,加總必須使用 long long 而非 int。
資料結構解
這題一看到就想到 STL 的 multiset 這東西,對兩種 key 各建一個 multiset,,insert, erase 新增刪除,begin 求最小,find 找特定值(或確定存在的話 lower_bound 也行),upper_bound 找第一個大於的值,直接收工。不確定出題者是不是沒考慮到這個資料結構,以歷屆來看,第三題不該能幾乎不思考硬砸單一內建函式或資料結構直接過的。
時間複雜度 O(n log n),常數稍大,看了下範圍 3e5,可行。
Sample Code
#include <iostream>
#include <set>
using namespace std;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n, t;
while(cin >> n >> t) {
long long a[n];
multiset<pair<long long, int>>s;
multiset<pair<int, long long>>st;
for(int i=0; i<n; i++) {
cin >> a[i];
s.insert({a[i], i});
st.insert({i, a[i]});
}
long long ans = 0;
while(!s.empty()) {
auto [x, i] = *s.begin();
if (x > t) break;
ans += x;
s.erase(s.begin());
auto it = st.upper_bound({i, x});
if (it != st.end()) {
auto [y, j] = *s.find({it->second, it->first});
s.erase({y, j});
s.insert({y+x, j});
st.erase(it);
st.insert({j, y+x});
}
st.erase({i, x});
}
cout << ans << endl;
}
}標準解
觀察一下題目,會發現難點是:
- 如何找到當前最小沙包和他的 index
- 如何找到並更新距離他最近的非空關卡
對於 1,直覺 set 或是某種 binary tree,但想得到 set 應該會去砸上面的 multiset,每次都找最小這個特性可以想到 min heap,也就是 STL 的 priority_queue。
對於 2,pq 做不到更新中間節點這件事,我們可以發現值只會變大不會變小,那直接把新值塞到 pq 內、每次取出時比對是否是最新的值就好啦!最新的值的維護可以用 map,歸 0 的記得 erase,這樣用 upper_bound 就能找到下一個非 0 index 了!
Sample Code
#include <iostream>
#include <queue>
#include <map>
using namespace std;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n, t;
while(cin >> n >> t) {
priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long, int>>>q;
map<int, long long>mp;
long long a[n];
for(int i=0; i<n; i++) {
cin >> a[i];
q.push({a[i], i});
mp[i] = a[i];
}
long long ans = 0;
while(!q.empty()) {
auto [x, i] = q.top();
q.pop();
if (x > t) break;
if (!mp.count(i) || x != mp[i]) continue;
ans += x;
mp.erase(i);
auto it = mp.upper_bound(i);
if (it != mp.end()) {
mp[it->first] += x;
q.push({mp[it->first], it->first});
}
}
cout << ans << endl;
}
}優化解
實際上,我們對每個關卡,只要他不超過限制重量,就一定會搬到 index 大於他的關卡中第一個 >= 他重量的(小於的都比他早搬完),且每個關卡會疊加的沙包肯定是從 index 比他小的地方來的。
發現這個性質後,題目可以轉換為對於每個 index i,找到第一個沙袋數大於等於他的 index j,處理到 index j 時要注意一下記得不要忘記前面來的值。太抽象的話上個圖:
範例一畫出來後
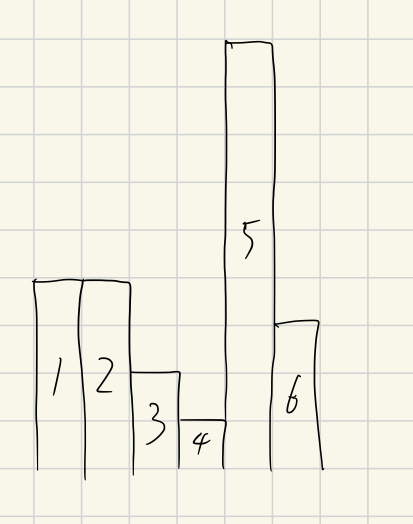
每個都往右邊第一個大於等於他的關卡搬動
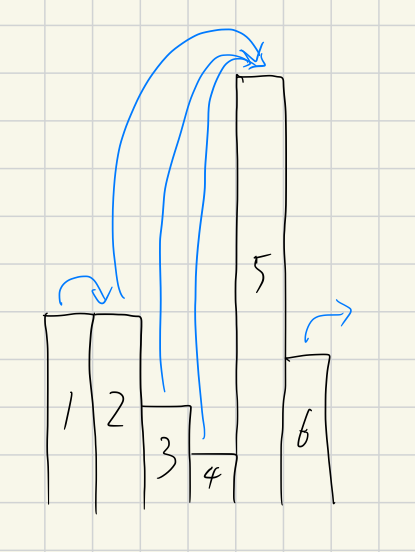
處理到自己時,就能知道累積沙袋數是多少
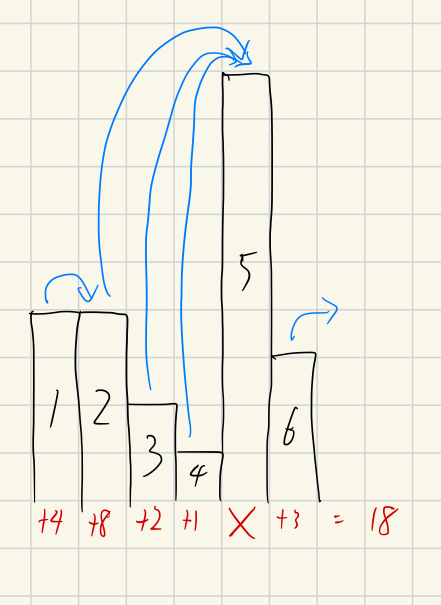
這看起來完全可以用一個遞減的 stack 實作:反向從「被放東西的關卡」思考,到 index j 時,看前面有多少東西會過來,即可知道到自己時有多少沙袋。
Sample Code
#include <iostream>
#include <stack>
#include <climits>
using namespace std;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n, t;
while(cin >> n >> t) {
long long a[n], ans = 0;
stack<long long>stk;
stk.push(LLONG_MAX);
for(int i=0; i<n; i++) {
cin >> a[i];
while(stk.top() <= a[i]) {
ans += stk.top();
a[i] += stk.top();
stk.pop();
}
if (a[i] <= t) {
stk.push(a[i]);
}
}
while(stk.size() > 1) {
ans += stk.top();
stk.pop();
}
cout << ans << endl;
}
}P4. 分組遊戲
Zerojudge 連結:https://zerojudge.tw/ShowProblem?problemid=q839
解題思路
對於競賽選手來說,應該一眼看得出來是裸的最小生成樹,那如果只學過圖論、完全沒做過這種題目,要怎麼聯想呢?
首先,把題目的圖畫出來
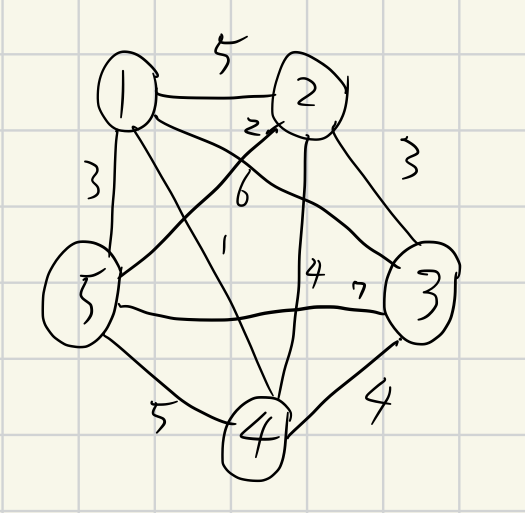
題目要求的分成 k 組這件事,實際上就是把一堆邊拔掉後,看剩餘有幾個連通塊(幾組)圖。
至於題目要的是分組後,剩餘的邊中的最小值要是最大的。拔邊這件事有點難,那如果我們先把 n 個點看成 n 個連通塊呢?會發現每加一個邊,在圖看成樹意即沒有 circle 的情況,其實就是讓連通塊少 1,也就是我們找到 n-k 條邊時,連通塊數量剛好是 k 個!
以貪心法的角度出發,我們其實可以直接找當前最小、不會製造出 circle 的邊,這樣當做出第 n-k 條邊時,下一條要被加入的邊,就是我們想尋找的最小邊最大值了!
加入一條邊,有四個連通塊。
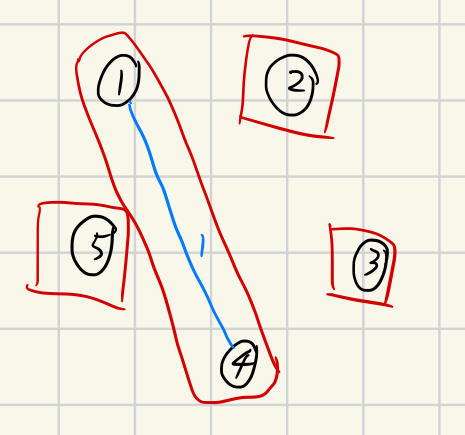
加入第二條邊,有三個連通塊。
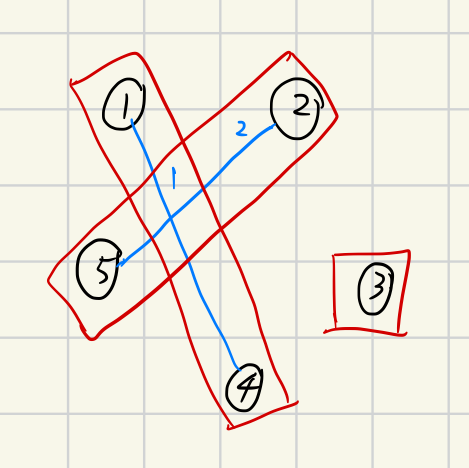
(5 - 3) = 2,下一條要加入的邊就是答案!
即使有多個相同權重的邊,不論加入哪一條,都會剩下兩個連通塊。
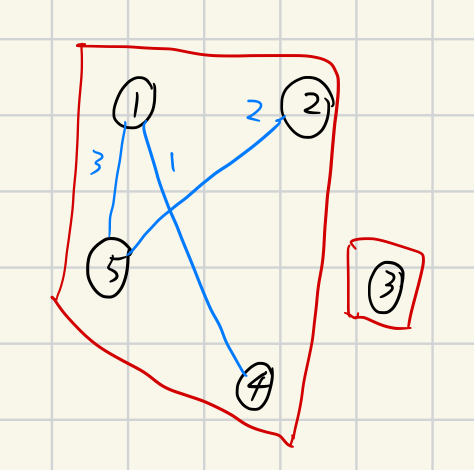
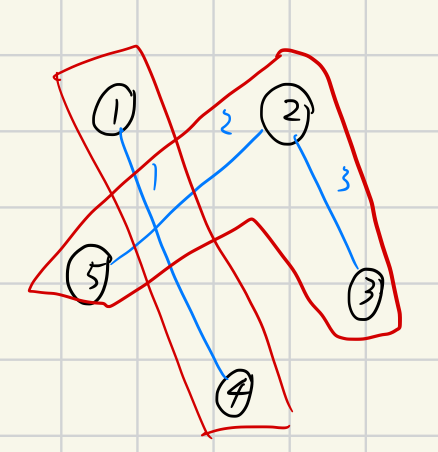
至於怎麼尋找不會製造出 circle 的邊呢?可以直接紀錄每個點所在的連通塊編號,當想加入的邊所連接的兩個點在同個連通塊,就代表會有 circle,直接不加入即可。
Sample Code
#include <iostream>
#include <queue>
#include <tuple>
using namespace std;
int gp[501];
int find(int x) {
if (x == gp[x]) return x;
return (gp[x] = find(gp[x]));
}
void merge(int x, int y) {
x = find(x);
y = find(y);
if (x != y) gp[x] = y;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n, k;
while(cin >> n >> k) {
int arr[n][n];
priority_queue<tuple<int, int, int>>edge;
for(int i=0; i<n; i++) {
gp[i] = i;
for(int j=0; j<n; j++) {
cin >> arr[i][j];
if (j > i) edge.push({-arr[i][j], i, j});
}
}
int t = n - k;
for(; t; ) {
auto [v, x, y] = edge.top();
edge.pop();
if (find(x) == find(y)) continue;
merge(x, y);
t--;
}
while(!edge.empty()) {
auto [v, x, y] = edge.top();
if (find(x) == find(y)) {
edge.pop();
continue;
}
cout << -v << endl;
break;
}
}
}